- aleanum1.pas
-
Cálculo de todas las constantes k admisibles para una
dada cubeta B (potencia de 2), cuando se efectúa una
búsqueda sistemática desde k=1, tarea anidada en un
lazo sobre las potencias de 2, desde Bmin=2 hasta
Bmax>2. La suma módulo 2, bit a bit, se hace mediante
la operación lógica ``xor'', que da verdadero
únicamente cuando ambas entradas son distintas.
- altura.pas
-
Dado un árbol calcular su altura.
- antecesor.pas
-
Suponga que se tienen los arreglos ORD_PRE [n],
ORD_SIM [n] y ORD_POS [n] que dan las posiciones en
los órdenes previo, simétrico y posterior,
respectivamente, de cada nodo n de un árbol ordenado
y orientado. Describa un algoritmo que diga si un nodo
i es un antecesor o no de un nodo j, para cualquier
par de nodos i, j e incluya los casos de antecesores
propios e impropios. Explique cómo trabaja
el algoritmo.
- arbbini.pas
-
Representación de arboles binarios por cursores al
padre e hijos. keywords: arbol binario
- aritme_arb.pas
-
Evalua expresiones algebraicas: primero genera el
árbol binario para una expresión algebraica
ingresada por teclado y luego la calcula.
keywords: arbol binario
- aritme_pil.pas
-
Evalua expresiones aritméticas en notación postfija
utilizando una pila. keywords: pila
- aritme_pilpre.pas
-
Evalua expresiones aritméticas en notación prefija
utilizando una pila. keywords: pila
- bilistado.pas
-
El `bi-listado' de un arbol ordenado orientado puede
pensarse como una combinacion de los listados previo y
posterior. Asumamos que las etiquetas tienen dos partes,
una etiqueta `derecha' y otra `izquierda', entonces el
bi-listado de un nodo n se define como:
BI_LISTADO (n) = (ETIQUETA_IZQUIERDA (n), BI_LISTADO(h1),
BI_LISTADO (h2), ... ETIQUETA_DERECHA (n)),
donde h1,h2 ... son los hijos de n. Por ejemplo, si
A:1 ( 8 ( 3 2 ) 4 ( 9 2 ) ), y tomamos como etiqueta centro
a (100+etiqueta) y etiqueta izquierda como (200+etiqueta),
entonces debe listar (10 21 121 30 40 140 51 60 160 70 170
151 80 180 130 110). Para simplificar, en vez de tener 2
etiquetas tenemos una sola etiqeta entera `e' y la etiqueta
derecha es 100+e. Por ejemplo si la etiqueta es 11 entonces
las etiquetas izquierda y derecha son [11,111].
[Tomado 2do parcial de 2003, 3-Jun-2003]
Keywords:arbol orientado
- bubl.pas
-
Escribir un procedimiento procedure BURBUJA(var L:lista); que
ordena los elementos de una lista L mediante el metodo de
clasificacion por burbujas. Como en listas simplemente enlazadas no
es conveniente avanzar hacia el principio de la lista por una
cuestion de eficiencia, el algoritmo de burbuja se modifica de
manera de que los elementos mas grandes viajan hacia el fin.
[Tomado 2do Parcial de 2003, 3-Jun-2003]
Keywords: lista, clasificacion
- busca.pas
-
Dadas dos listas L1,L2 de longitud n1, n2 determinar si la lista L2
contiene una sublista igual a L1, es decir, si existe un conjunto de
indices INDX(1),<INDX(2)<...<INDX(n1) tales que L2(INDX(1)) = L1(1),
L2(INDX(2))=L1(2) .... L2(INDX(n1))=L1(n1). Consigna: escribir una
funcion `function L1,L2 : lista; var INDX: lista): boolean ;' tal que
si L2 contiene a L1 como una sublista, entonces debe retornar `true' y
en `INDX' debe retornar los indices en L2 que componen L1. Si L2 no
contiene a L1 entonces debe retornar `false' e INDX debe estar vacia.
[Tomado en el final del 8-Aug-2003.] keywords: lista
- cadenapq.pas
-
Determinar si una cadena z es de la forma z = x C y,
donde y es la cadena inversa de x. Se usan los
TAD-PILA y TAD-COLA de caracteres por punteros.
keywords: pila, cola
- caminoord.pas
-
Dado un arbol ordenado binario A y un nodo n escribir una funcion
CAMINO_ORD(n: nodo, A:arbol): boolean; que retorna verdadero si existe
algun camino ordenado desde n a una hoja en el subarbol del nodo
n. Por ejemplo en el caso del arbol de la izquierda en la figura de
abajo debe retornar true ya que el camino marcado con lineas de puntos
esta ordenado de menor a mayor yendo desde la raiz a la hoja, mientras
que para el de la derecha debe retornar false ya que no existe ningun
camino con esas caracteristicas. Se sugiere el siguiente algoritmo: Un
dado nodo n debe retornar true si, o bien es una hoja, o bien alguno
de sus hijos c contiene un camino ordenado y ETIQUETA(c)>ETIQUETA(n).
[Tomado 2do parcial de 2003, 3-Jun-2003]
keywords: arbol binario
- concatena.pas
-
Escriba un programa para concatenar dos listas de enteros
L1 y L2 en una nueva lista L3. Esta solución
llama primero al procedimiento COPIA para copiar la
primera lista L1 en la lista L3 y, luego, apendiza
la lista L2 al final de L3.
Esta versión usa la unidad 'u_listpi', es decir, listas
de enteros por punteros y sin puntero a la celda final.
keywords: lista
- conjchar.pas
-
Programa de prueba para conjuntos de caracteres
por arreglos de bits. keywords: conjunto
- copia.pas
-
Ejercicio tomado en el 2do parcial/2001, tema 1:
escribir una función COPIA (n:nodo): nodo, que devuelva
la copia del árbol ordenado cuya raiz es apuntada
por el cursor n pasado como argumento. La función usa
un array COPIA_HIJOS de cursores a nodo. Asumir que cada
nodo tiene a lo sumo 4 hijos.
- cuentaalt.pas
-
Escribir una función function CUENTA_ALT(n:nodo; m:integer; A:arbol)
: integer; que dado un nodo n en un árbol A cuenta el número de
nodos del subárbol de A cuya raiz es n tales que la altura de su
subarbol es de altura menor o igual que m. [Tomado en el Examen
Final del 27 de febrero de 2003] Keywords: arbol orientado
- cuentaprof.pas
-
Escribir una function CUENTA_PROF (n: nodo; m: integer;
A: arbol): integer; que dado un nodo n en un árbol A
cuenta el número de nodos del subárbol de A cuya
raiz es n y que están a profundidad m o menor (con
respecto a n). [Tomado en el Examen Final del 11 de
julio de 2002] keywords: arbol
- escompleto.pas
-
Ejercicio tomado en el Exámen Final del 28/2/2002:
se dice que un árbol binario es completo si cada nodo del
mismo o bien es una hoja o bien tiene sus dos hijos.
Escribir una función recursiva ES_COMPLETO (a: arbol) :
boolean, la cual retorna verdadero si el árbol binario 'a'
es completo. Usar las funciones de árbol binario:
HIJO_IZQUIERDO (n), HIJO_DERECHO (n), ETIQUETA (n).
keywords: arbol binario
- evalua.pas
-
Dado un árbol binario que representa una expresión
matemática, retorna el resultado.
keywords: arbol binario
- huffman.pas
-
Calcula códigos de Huffman. keywords: arbol binario
- iguales.pas
-
Ejercicio tomado en el 2do parcial/01: verificar si dos
árboles ordenados y orientados son iguales, es decir,
si tienen la misma estructura y contenido.
keywords: arbol orientado
- incluido.pas
-
Ejercicio tomado en el Exámen final del 14/12/01:
escribir una función INCLUIDO (B, A: nodo) : boolean, la
cual retorna verdadero si la estructura del árbol B
está incluida dentro de la del árbol A. Definiendolo
en forma recursiva, un árbol B está incluido en otro
A si: (B=Lambda) or (A<>Lambda). La estructura de los
hijos de B está incluida en la estructura de los
correspondientes hijos de A. Se pide:
(a) Explicar el significado de la condición
(B=Lambda) or (A<>Lambda);
(b) Escribir el procedimiento function INCLUIDO (B,A: nodo):
boolean, utilizando las funciones PADRE (n,A),
HIJO_MAS_IZQUIERDO (n,A), HERMANO_DERECHO (n,A),
ETIQUETA (n,A), CREA0 (v), CREA1 (v,A1), CREA2 (v,A1,A2).
- intercala1.pas
-
Escriba un procedimiento para intercalar dos listas
ordenadas L1 y L2 en una nueva lista L también ordenada.
Esta versión se copia todo L1 en L3 y después se usa
INSERTA_ORD para poner los elementos de L2 en los lugares
correctos de L (ver también ``intercala2.pas'').
keywords: lista
- intercala2.pas
-
Escriba un procedimiento para intercalar dos listas
ordenadas L1 y L2 en una nueva lista L también
ordenada. Esta versión se mantienen dos punteros sobre
cada una de las listas y se va copiando siempre el
elemento menor y actualizando el puntero correspondiente
(ver también ``intercala1.pas'').
keywords: lista
- intercambi.pas
-
Escribir un procedure INTERCAMBIA (var L:lista); que
intercambia los elementos de L de tal forma que aquellos
que están en una posición impar son intercambiados con
el elemento en la posición par inmediatamente siguiente.
Es decir, el primero es intercambiado con el segundo, el
tercero con el cuarto y asi siguiendo. Si el número de
elementos es impar, entonces el ultimo elemento queda
inalterado. Asi por ejemplo, si la listas es
L=(10 1 15 7 2 19 15 16 11 15 9 13 3 7 6 12 1)
entonces después de intercambiar debemos tener
L=(1 10 7 15 19 2 16 15 15 11 13 9 7 3 12 6 1).
(Ejercicio tomado en el examen final de 9/5/2002).
keywords:lista
- imprinv.pas
-
Escriba un procedimiento para imprimir de forma recursiva
una lista invertida. Se le da como dato al procedimiento
el primer nodo de la lista. Ejercicio 3 del final del
14/02/2002. Esta version usa la unidad u_listpi (listas de
enteros por punteros y sin puntero a la celda final).
keywords:lista
- invierte.pas
-
Dada una lista L1, escribir un procedimiento INVIERTE que
retorna la lista con sus elementos en orden invertido.
keywords: lista
- jose_cif.pas
-
Resolución del problema de Josephus mediante TAD-LISTA
de enteros por cursores y con celdas de encabezamiento.
- jose_lai.pas
-
Resolución del problema de Josephus mediante TAD-LISTA
de enteros por arreglos.
- jose_lci.pas
-
Resolución del problema de Josephus mediante TAD-LISTA
de enteros por cursores y sin celdas de encabezamiento.
- jose_lpi.pas
-
Resolución del problema de Josephus mediante TAD-LISTA
de enteros por punteros y con celdas de encabezamiento.
- junta.pas
-
Escribir un procedure JUNTA (var L: lista; m: integer);
que dada una lista L, agrupa de a "m" elementos dejando
su suma. Por ejemplo si la lista L contiene
L = (1,3,2,4,5,2,2,3,5,7,4,3,2,2), entonces depués de
JUNTA (L,3) debe quedar L = (6,11,9,14,4).
Prestar atención a no usar posiciones inválidas
después de una supresión. El algoritmo debe tener
un tiempo de ejecución O(n), donde n es el número
de elementos en la lista original.
[Tomado en el examen final del 1/8/2002]
keywords: lista
- kmenores.pas
-
Encontrar los k enteros menores en un arreglo de longitud
n. Se hace o bien búsqueda del minimo k veces o
bien clasificación rápida (quicksort), según sea
k con respecto a log(n).
keywords: clasificacion
- lexico.pas
-
Ejercicio tomado en el 1er parcial 16/04/02.
Dadas dos listas de enteros L1 y L2, escribir una
function LEXICORD (L1, L2: lista): boolean, que retorna
true si la lista L1 es mayor que la L2 en sentido
lexicográfico, y false en caso contrario. El orden
lexicográfico es el orden alfabético y puede
definirse de la siguiente manera:
1) si las dos listas son vacias, entonces son iguales
(valor de retorno false);
2) si L1 es vacia y L2 no lo es, entonces L1 < L2 es falso;
3) si L2 es vacia y L1 no lo es, entonces L1 < L2 es true;
4) Si las dos listas no son vacias, y los primeros
elementos son diferentes (digamos a_1 y b_1),
entonces el valor de retorno es a_1 > b_1.
Si los dos primeros elementos fueran iguales,
entonces el valor de retorno será el
correspondiente a las listas que se obtienen
eliminando los primeros elementos.
Asi, por ejemplo,
a) Si L1 = [1 3 2 4 6] y L2 = [1 3 2 5], entonces L2 > L1
y LEXICORD (L1, L2) retorna false;
b) Si L1 = [1 3 3 4 5] y L2 = [1 3 3], entonces L1 > L2 y
LEXICORD (L1, L2) retorna true;
c) Si L1 = [1 3 3 4] y L2 = [1 3 3 4], entonces L1 = L2 y
LEXICORD (L1, L2) retorna false.
keywords: lista
- listarbb.pas
-
Listado de árboles binarios en diferentes ordenes.
keywords: arbol binario
- listarbo.pas
-
Listado de árboles orientados en diferentes ordenes.
keywords: arbol orientado
- matrices.pas
-
Escribir un procedimiento Pascal que, dada una lista de los indices de
una serie de matrices M1, M2, ..., Mn, calcula el orden optimo (o
cuasi-optimo) en el cual se deben realizar las multiplicaciones para
minimizar el numero de operaciones. Asuma que la multiplicación de
una matriz de p x q por otra de q x r requiere z = p q r operaciones
escalares (que es el número de operaciones requerido por el
algoritmo de multiplicación de matrices). Si M1 es de p1 x q1, M2 es
de p2 x q2 .... y Mn es de pn x qn, entonces la lista L contiene los
indices L=(p1,p2,p3,...,pn,qn). Notar que los q1, q2, ..., q(n-1) no
son necesarios ya que debe ser q1=p2, q2=p3, ..., q(n-1)=pn.
keywords: algoritmos
- maxarbb.pas
-
Operaciones varias con árboles binarios
(ver ``maxarbo.pas'' para las mismas
operaciones con árboles orientados):
1) CANT_NOD: cantidad de nodos;
2) PROF_NOD: profundidad de un nodo (cuando el nodo es el
nodo raiz, entonces su profundidad es la profundidad
del árbol y coincide con su altura);
3) SUMA_ETIQ: suma de las etiquetas;
4) CTOS_PARES: cantidad de nodos con etiqueta par;
5) PROF_PAR: profundidad del árbol teniendo en cuenta
solamente los nodos con etiqueta par;
6) MAX_ETIQ: máximo de las etiquetas, asumiendo que
todas son positivas.
7) MAXIMO_PAR: máxima etiqueta par.
keywords: arbol binario
- maxarbo.pas
-
Operaciones varias con árboles orientados:
(ver ``maxarbb.pas'' para las mismas
operaciones con árboles binarios):
1) CANT_NOD: cantidad de nodos;
2) PROF_NOD: profundidad de un nodo (cuando el nodo es el
nodo raiz, entonces su profundidad es la profundidad
del árbol y coincide con su altura);
3) SUMA_ETIQ: suma de las etiquetas;
4) CTOS_PARES: cantidad de nodos con etiqueta par;
5) PROF_PAR: profundidad del árbol teniendo en cuenta
solamente los nodos con etiqueta par;
6) MAX_ETIQ: máximo de las etiquetas, asumiendo que
todas son positivas;
7) MAXIMO_PAR: máxima etiqueta par.
keywords: arbol orientado
- maxhoja.pas
-
a) Escribir un procedure HOJAS (A: arbol; n: nodo);
que lista las etiquetas de las hojas de un árbol
ordenado orientado. Por ejemplo, en el
árbol (142 (63 (33) 42 (23 7 35)) 48 125 (130 12))
debe listar: 33 23 7 35 48 130 12.
b) Escribir una function MAXHOJA (A: arbol; n: nodo):integer;
que retorna el máximo de las etiquetas de las hojas
de un árbol ordenado orientado. Por ejemplo, en el
árbol (142 (63 (33) 42 (23 7 35)) 48 125 (130 12))
debe retornar 130.
keywords: arbol orientado
- maxcota.pas
-
Escribir una función ``function
MAXCOTA (n: nodo; A: arbol; cota: integer): integer;'' que
retorna el máximo de las etiquetas de un árbol binario
tales que son menores o iguales que la cota c. Por ejemplo,
si las etiquetas de un árbol A son (1,3,7,4,2,10,13) y
cota=8, entonces MAXCOTA (raiz (A), A, 8) debe retornar 7.
keywords: arbol orientado
- maxdevm.pas
-
Dada una secuencia de numeros (a_1,a_2,...,a_n), vamos a
decir que su "maxima desviacion", es la maxima
diferencia (en valor absoluto) entre todos sus numeros:
maxdev(a_1,a_2,...,a_n) = max_(j=1,n) a_j - min_(j=1,n) a_j
Escribir una funcion "function MAX_DEV_M(L:lista; m:integer) :
integer;" que retorna el maximo de las maximas desviaciones de las
subsecuencias de L de longitud m.
Por ejemplo, si (1,3,5,4,3,5), entonces MAX_DEV_N(L,3)
debe retornar 4 ya que la maxima desviacion se da en la primera
subsecuencia (1,3,5) y es 4. Se sugiere el siguiente algoritmo,
para cada posicion p en la lista hallar la maxima
desviacion de los m elementos siguientes (incluyendo a
p). Hallar la maxima de estas desviaciones. Keywords: lista
- menor.pas
-
Dada una lista de ciudades y una función DISTANCIA que
retorna la distancia entre dos ciudades dadas, busca el
camino de menor recorrido, utilizando un algoritmo
heuristico. keywords: algoritmos
- mrgsrt.pas
-
El algoritmo Mergesort modificado. El procedimiento Mergesort
se basa en la estrategia "dividir para vencer". Primero se
ordenan las posiciones impares entre si (recursivamente),
luego las pares y, finalmente, se intercalan ambas
subsecuencias. Si el intercalamiento se puede hacer en
tiempo O(n) entonces puede demostrarse que el número de
operaciones total es O(n log(n)) en el peor caso. Ya hemos
visto para la representación de conjuntos como listas
enlazadas clasificadas que el intercalamiento de dos listas
enlazadas clasificadas se puede hacer en tiempo O(n).
Para vectores no es tan sencillo, y se conjetura que no se
puede hacer tal operación en tiempo O(n) sin uso de
memoria adicional (es decir, no se puede hacer "in place").
Escriba un `procedure MERGEQ (var A:vector; N:tipo_elemento);'
que ordena un vector cuyas posiciones pares e impares
están ordenadas entre si, usando una cola auxiliar.
[Tomado en el 3er parcial 2002 (25 de junio de 2002)]
keywords: clasificacion
- mrgsrtc.pas
-
Escribir un procedimiento procedure MERGESORT(var L:lista); que ordena
los elementos de una cola usando el metodo de clasificacion por
intercalacion. Es decir, divide la cola en dos subcolas auxiliares
C1 y C2 de tamano similar, las ordena aplicando MERGESORT
recursivamente y luego intercala las subcolas: a) dividir C en dos
subcolas C1, C2, b) clasificar C1 y C2 por MERGESORT , c) intercalar
C1 y C2 en C. [Tomado 2do parcial de 2003, 3-Jun-2003] Keywords:
clasificacion, cola
- mrgsrtl.pas
-
Escribir un procedimiento
procedure MERGESORT(var L:lista); que ordena los elementos de una
lista usando el metodo de clasificacion por intercalacion. Es
decir, divide la lista en dos sublistas auxiliares L1 y L2 de
tamano similar, las ordena aplicando MERGESORT recursivamente y
luego intercala las sublistas: a) dividir L en dos sublistas L1, L2,
b) clasificar L1 y L2 por MERGESORT , c) intercalar L1 y L2 en L.
[Tomado 2do parcial de 2003, 3-Jun-2003]
Keywords: clasificacion, lista
- multirec.pas
-
Escribir un procedimiento procedure MULTI_REC(L1,IND: lista; var L2:
lista); que, dados una lista L1 y otra lista IND de indices enteros,
retorna los elementos de la lista L1 que están en las posiciones
indicadas por los números en IND. Se asume que los indices en IND
son crecientes, es decir IND(j)<= IND(j+1), para todo j.
Por ejemlo, si L1=(6,4,8,1,8,2,7,3,1,2,10,1) y IND=(1,1,4,6,10,12),
entonces MULTI_REC(L1,IND,L2); debe retornar L2=(6,6,1,2,2,1).
[Tomado en el final del 8-May-2003.]
keywords:lista
- oparboles.pas
-
Diversas operaciones con árboles binarios:
CREA_DE_STRING: permite ingresar árboles con
``a(b,c(d,r))'';
IMPRIME_S: imprime en el mismo formato;
SEMEJANTE: determina si la estructura de dos árboles
es la misma;
ES_ESPEJO: determina si la estructura de un árbol es
la espejada de otro;
IGUALES: determina si dos árboles son iguales,
en estructura y contenido;
INCLUIDO: determina si la estructura de un árbol
está contenido en la de otro;
COPIA: copia un árbol en otro;
COPIA_ESPEJO: copia un árbol en otro en forma espejada;
INTERSECCION: determina aquella parte de la estructura
que es común a dos árboles.
keywords: arbol binario
- ordena.pas
-
Ejercicio tomado en el Examen Final del 27/9/01:
``Numeración de Cuthill-Mc Kee''.
Una red de computadoras tiene una serie de nodos
a,b,c,...,n (ver figura) y se quiere conocer el
orden en el que se irán infectando los nodos en
el caso de que uno de ellos se infecte con un virus.
Suponiendo que el primero en infectarse es el nodo n,
entonces éste infectará, en primera instancia, a los
nodos g,k,j (primera 'capa de vecinos'), los cuales
están conectados a él. Luego, estos nodos infectarán
a los nodos h,c,b,l ('segunda capa'), estos a la tercera
capa a,f,i,m y, finalmente, estos a la 4ta capa, la cual
consiste solamente del nodo e. Se tiene la información
de la red en un vector de listas: vecinos: array [1..nnod]
of lista, y se pide escribir un procedimiento
INFECTA (vecinos, primero, orden) el cual, dado un nodo
`primero', retorna los nodos en una lista, segun el orden
en que se pueden ir infectando. Los nodos dentro de una
misma capa pueden aparecer en cualquier orden entre si.
keywords: algoritmos
- ordenag.pas
-
[Tomado en el examen final del 5-Dic-2002].
Escribir un procedure ORDENAG (var L: lista; m:integer);
que dada una lista L va ordenando sus elementos de
a grupos de "m" elementos. Por ejemplo si m=5, entonces
ORDENAG ordena los primeros 5 elementos entre si, después
los siguientes 5 elementos, y asi siguiendo. Si la
longitud N de la lista no es un múltiplo exacto de "m",
entonces los ultimos (N mod m) elementos también
deben ser ordenados entre si. Por ejemplo, si
L=(10 1 15 7 2 19 15 16 11 15 9 13 3 7 6 12 1),
entonces después de ORDENAG (L, 5) debemos tener
L=(1 2 7 10 15 11 15 15 16 19 3 6 7 9 13 1 12).
keywords: lista
- ordnivel.pas
-
Imprime el orden de nivel de un arbol ordenado.
Utiliza una cola auxiliar para construir el orden
de nivel. keywords: arbol orientado, cola
- ordnodo.pas
-
Escribir una function ORDNODO (n: nodo, A:arbol): boolean;
que verifica si cada secuencia de hermanos del subarbol
del nodo "n" (perteneciente al arbol ordenado orientado A)
estan ordenadas entre si, de izquierda a derecha. Por
ejemplo, ver figura, para el arbol de la izquierda deberia
retornar "true", mientras que para el de la derecha deberia
retornar "false", ya que las secuencias de hermanos
indicados en las rayadas NO estan ordenados. Se sugiere el
siguiente algoritmo: para un dado nodo retornar false si:
1) sus hijos no estan ordenados o 2) algunos de sus hijos
contiene en su subarbol una secuencia de hermanos no
ordenada (recursividad).
[Tomado 2do parcial de 2003, 3-Jun-2003]
keywords: arbol orientado
- palindro1.pas
-
Ejercicio tomado en el Exámen Final del 30/7/2001:
dado un string verificar si es un palindromo.
- parcord.pas
-
Se dice que un árbol binario es `parcialmente ordenado'
(PO) si la etiqueta de cada nodo es menor o igual que las
etiquetas de sus hijos. Así por ejemplo, el árbol
1(2,3(4,5)) es parcialmente ordenado, pero el 5(2,3(4,5))
no lo es porque 5 es mayor que su hijo 2.
Entonces, escribir una
función `VERIFICA_PO(n:nodo; A: Arbol): boolean' que
retorna `true' si el subárbol que cuelga del nodo n es
parcialmente ordenado y `false' en caso contrario. Usar
las primitivas del `TAD ARBOL BINARIO:', `HIJO_IZQ(n,A)',
`HIJO_DER(n,A)', `ETIQUETA(n,A)'.
[Tomado en el segundo parcial del cursado 2002, 28/5/2002]
keywords: arbol binario
- parentesis.pas
-
Control de paréntesis en una expresión algebraica
usando TAD-PILA de caracteres por punteros. Por
``parentización'' en una expresión algebraica
consideramos los simbolos: paréntisis, corchetes y
llaves.
La cadena leida (caracter a caracter) puede contener otros
simbolos. Pero, para el control, prestamos atención
sólo a los caracteres de parentización, de los cuales:
a) si el simbolo leido es ``abierto'', entonces se lo
almacena a la espera de encontrar un ``cerrado'';
b) si el simbolo leido es ``cerrado'', entonces se
determina si el ULTIMO simbolo ``abierto'' almacenado
es del mismo tipo. Si lo son, entonces ambos parentizan
correctamente, no hace falta considerarlos ulteriormente,
y se prosigue evaluando el resto de la cadena. Si no lo
son, entonces, la cadena estará mal parentizada.
En consecuencia, el TAD a usar sera tal que ``el último en
entrar, es el primero en salir'', o sea, una PILA.
keywords: pila
- parimpa.pas
-
Escribir un procedimiento ENCOLAR_TRABAJO que, dado un
código de trabajo n lo pone o bien en la cola par,
o bien en la cola impar, dependiendo del número.
Escribir un procedimiento SIGUIENTE_TRABAJO que obtiene el
siguiente trabajo a procesar, dando mayor prioridad a la
cola par. keywords: cola
- particiona.pas
-
Ejercicio tomado en el Exámen Final del 05/07/01:
1) Usando las operaciones de Lista, escribir un procedimiento
PARTICIONA (var L: lista; a: integer) el cual, dada una
lista de enteros L reemplace aquellos que son mayores que
`a' por una sucesión de elementos menores o iguales que
`a' manteniendo la suma total constante. Se propone el
siguiente algoritmo: recorrer la lista y, cada vez que se
encuentra un elemento `x>a' suprimirlo y reemplazarlo por
`a' tantas veces como entren en `x' y finalmente el resto,
por ejemplo, si `x=7' y `a=2', entonces se debe reemplazar
ese 7 por la secuencia `2,2,2,1'. En la lista final NO deben
quedar elementos mayores que `a'. Por ejemplo, si
L=[2,5,2,6,4,1,9,6,3,2], entonces PARTICIONA (L,4) debe
retornar L=[2,4,1,2,4,2,4,1,4,4,1,4,2,3,2];
2) Usando las operaciones de Lista, escribir un procedimiento
REJUNTA (var L: lista; a: integer) que, dada una lista de
enteros L, agrupe elementos de tal manera que en L queden
solo elementos mayores o iguales que `a'. El algoritmo
recorre la lista y, cuando encuentra un elemento menor,
empieza a agrupar el elemento con los siguientes hasta
llegar a `a' o hasta que se acabe la lista. Por ejemplo,
si L=[3,4,2,4,1,4,4,3,2,2,4,1,4,1,4,4,1,4,4,2], entonces
REJUNTA (L,10) da L=[13,12,13,10,10]. En la lista final
NO deben quedar elementos menores que `a' salvo,
eventualmente, el último.
keywords: lista
- pila2.pas
-
Tareas simples sobre el TAD-PILA.
- pru_cpi.pas
-
Prueba implementación de colas de enteros por punteros.
keywords: cola, punteros
- pruarbp.pas
-
Prueba arboles enlazados por punteros.
keywords: arbol orientado, punteros
- pru_ppi.pas
-
Prueba implementación de pilas de enteros por punteros.
keywords: pila, punteros
- prueba_cif.pas
-
Prueba implementación de listas de enteros por cursores
para la versión ``u_liscif'' con celda de encabezamiento
y cursor al final. keywords: lista, cursores
- prueba_lai.pas
-
Prueba implementación de listas de enteros por
arreglos, para la versión ``u_listai''.
keywords: lista, arreglos
- prueba_lci.pas
-
Prueba implementación de listas de enteros por cursores
para la versión ``u_listci'' sin celda de encabezamiento.
- prueba_lpi.pas
-
Prueba implementación de listas de enteros por punteros,
para la versión ``u_listpi'', es decir, sin puntero
a la celda final. keywords: lista, punteros
- prueba_pif.pas
-
Prueba implementación de listas de enteros por punteros,
para la versión ``u_listpif'', es decir, con un puntero
a la celda final y mejor manejo de memoria, esto es, hace
los `dispose' correspondiente en ANULA y en SUPRIME.
keywords: lista, punteros
- prueord2.pas
-
Prueba los métodos de ordenación: burbuja,
inserción, selección, Shell, monticulos y rápido.
keywords: clasificacion
- pruprique.pas
-
Prueba colas de prioridad.
keywords: cola de prioridad
- prusetli.pas
-
Programa de prueba para conjuntos representados
mediante listas. keywords: conjunto, lista
- prusha.pas
-
Prueba diccionario con tabla de dispersion abierta.
keywords: tabla de dispersion
- prushaci1.pas
-
Prueba operaciones sobre TAD-DICCIONARIO mediante
tablas de dispersión cerradas y con resolución lineal
de colisiones.
keywords: tabla de dispersion
- prushaci2.pas
-
Prueba operaciones sobre TAD-DICCIONARIO mediante
tablas de dispersión, ya sea lineal (redisp1) o bien
pseudo-aleatoria (redisp2).
keywords: tabla de dispersion
- purgaord.pas
-
Escribir un programa que elimina los elementos repetidos de
una lista ordenada.
keywords: lista
- ralea.pas
-
Dada una lista, retornar sus elementos ordenados en
forma pseudo-aleatoria.
keywords: lista
- refina.pas
-
(a) Escriba un procedimiento
REFINA (delta: real; var L:lista) tal que dada una lista
de reales clasificados de menor a mayor L, REFINA
inserta elementos entre los de L, de modo tal que la
diferencia máxima entre elementos de la lista final
sea menor o igual que delta;
(b) Escriba un procedimiento
DESREFINA (delta: real; var L:lista) tal que dada una
lista de reales clasificados de menor a mayor
L, REFINA suprime elementos entre los de L, de modo tal que
la diferencia minima entre elementos de la lista final
sea mayor o igual que delta.
- reemplaza.pas
-
[Tomado el 1er parcial, 16 abril 2002]. Dada una lista L
con enteros y dos listas S (por secuencia) y R (por
reemplaza) escribir un
procedure REEMPLAZA (var L: lista; S, R: lista)
que busca todas las secuencias de S en L y las
reemplaza por R. Ejemplo, si
L = (1 2 3 4 5 1 2 3 4 5 1 2 3 4 5), S = (4 5 1) y
R = (9 7 3), entonces despues de llamar a REEMPLAZA
debe quedar L = (1 2 3 9 7 3 2 3 9 7 3 2 3 4 5). Este
procedimiento tiene un efecto equivalente a la función
REEMPLAZAR de los editores de texto.
keywords: lista
- rotacion.pas
-
Ejercicio tomado en el 1er parcial, 16/04/02.
Escribir un procedimiento ROTACION (var C: cola), el cual
saca una cierta cantidad de enteros del frente de la cola
C y los vuelve a insertar en fin de la cola, de tal manera
que quede en el frente de cola un número par. Por ejemplo,
si C = [1, 3, 5, 2, 4] entonces, después de ROTACION (C),
debe quedar C = [2, 4, 1, 3, 5].
keywords: cola
- ruleta.pas
-
Ejemplo interesante para mostrar el uso de punteros.
Simula una ruleta creando una lista circular de 37
celdas enlazadas con punteros. Generando con la
función random un número pseudo-aleatorio n
entre 0 y 36, se avanza en la lista n.
- saca_fondo.pas
-
Ejercicio tomado en el 1er parcial 16/04/02.
Escribir un procedimiento SACA_FONDO (var P: pila) que
elimina el último elemento de una pila P, dejando
los demás inalterados, usando exclusivamente una
pila auxiliar. Por ejemplo, si P = [ 8 3 9 1 6 5 ],
después de SACA_FONDO (P), debe quedar
P = [ 8 3 9 1 6 ].
keywords: pila
- sacapar.pas
-
[Ejercicio tomado en el final del 13-Feb-2003].
Escribir un procedure SACAPAR (var L: lista; var C: cola);
que apendiza a la lista L todos los elementos de
C que son pares, los cuales a su vez deben ser
removidos de la cola C. Se puede usar una
estructura auxiliar (cola o lista). Por ejemplo, si
inicialmente L= (2,3,4) y C=(1,6,3,5,2,8)
entonces, despues de hacer SACAPAR (L,C) debe
quedar L=(2,3,4,6,2,8) y C=(1,3,5).
keywords: lista, cola
- secuencia.pas
-
Ejercicio tomado en el Examen Final del 26/7/01:
escribir un procedure SECUENCIA (L: lista; var L1: lista);
el cual busca la secuencia ordenada más larga dentro de
la lista L dada.
Ejemplo: si L=(5, 5, 4, 5, 4, 3, 5, 5, 6, 6), entonces
la secuencia ordenada más larga es L1=(3, 5, 5, 6, 6).
- semej_or.pas
-
Verificar si dos árboles ordenados y orientados son
semejantes, es decir, si independientemente de sus
contenidos, tienen la misma estructura.
[Ejercicio tomado en el 2do parcial 2001 y en el
recuperatorio globalizador 2-Julio-2002].
keywords: arbol orientado
- separa.pas
-
Escribir un procedimiento SEPARA que, dada una lista L,
devuelve los elementos de la lista reordenados de tal
manera que, primero, están los pares y, después, los
impares. Tanto los elementos pares como los impares deben
quedar en el mismo orden relativo entre si que tenian
previamente (en este caso se dice que el algoritmo es
`estable'). Por ejemplo, si L = [81, 16, 86, 37, 88, 29,
29, 47, 76, 59, 12, 49, 35], entonces despues de aplicar
SEPARA debemos tener L = [16, 86, 88, 76, 12, 81, 37, 29,
29, 47, 59, 49, 35]. Se sugiere el siguiente algoritmo:
recorrer la lista eliminando los elementos impares y
ponerlos en una cola auxiliar. Finalmente, insertar los
elementos de la cola al final de la lista.
keywords: lista
- suaviza.pas
-
Dada una lista de elementos (a1, a2, .... an) la hmaxima
diferencia de sus elementos es la diferencia entre el máximo y
el mínimo de sus elementos (max(i=1,..,n) a_i) - ((min i=1,..,n)
a_i). Escribir un procedimiento procedure SUAVIZA(var L:lista; m,
max_dif:integer);' que remueve aquellos elementos de L tales que la
maxima diferencia de una subsecuencia de longitud `m' es `max_dif'. Se
sugiere el siguiente algoritmo, para cada elemento `v' de la lista
recorrer la lista a partir de ese elemento y eliminar aquellos
elementos que son mayores que `v+max_dif' o menores que
`v-max_dif'. Este lazo interno termina cuando se han recorrido `m'
elementos o bien se llega al final de la lista.
- sumamult.pas
-
Ejercicio tomado en el Exámen Final del 26/7/2001:
Dado un arbol binario escribir una función que retorna
la suma de sus etiquetas y otro que retorna la suma de
aquellas etiquetas que son múltiplo de 3.
keywords: arbol binario
- sumaparantc.pas
-
Escribir una function SUMA_PAR_ANTEC (n:nodo; a:arbol):
integer; que devuelve la suma de las etiquetas de los
nodos tales que su etiqueta y la etiqueta de todos sus
antecesores sea par. En forma recursiva SUMA_PAR_ANTEC
es 0 si el arbol esta vacio o su etiqueta es impar y
en otro caso es la suma de su etiqueta mas la
SUMA_PAR_ANTEC de sus hijos.
keywords: arbol orientado
- stride.pas
-
Escribir un procedimiento
STRIDE (L1: lista ; var L2: lista; c, f, i: integer);
que retorna en L2 los elementos que ocupan las posiciones
desde el comienzo "c" hasta el final "f" (inclusive), a
intervalos "i", pero sin incluir las posiciones iguales
o mayores que FIN de lista. Es decir, debe retornar
los elementos en las posiciones: c, c+i, c+2*i, ...,
mientras éstas sean menores o iguales que "f" y estén
dentro del rango de posiciones válidas en la lista.
Por ejemplo, si L1 = (3,2,1,5,4,2,3,2,6) y llamamos
STRIDE (L1, L2, 2, 8, 3), entonces debe retornar
L2 = (2, 4, 2); mientras que si hacemos
STRIDE (L1, L2, 3, 20,4) debe retornar
L2 = (1,3) [Ejercicio tomado en el final del 27-Feb-2003].
keywords: lista
- tartaglia.pas
-
Cálculo del número combinatorio C (n,r) , donde
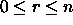 , usando el triángulo de Tartaglia
(o de Pascal) mediante:
i) un procedimiento (muy caro) basado en la siguiente
propiedad recursiva:
C (n,r) = 1 , si r=0 o r=n, sino
C (n,r) = C (n-1,r-1) + C (n-1,r) , en los
demás casos;
ii) un procedimiento por programación dinámica, en
donde directamente se construye el triángulo de
Tartaglia hasta el nivel requerido.
Por ejemplo, para el número combinatorio C (30,12)
constatamos k1=172.986.449 llamadas de recursión,
las cuales se reducen a k2=930 operaciones por
programación dinámica.
keywords: algoritmos
, usando el triángulo de Tartaglia
(o de Pascal) mediante:
i) un procedimiento (muy caro) basado en la siguiente
propiedad recursiva:
C (n,r) = 1 , si r=0 o r=n, sino
C (n,r) = C (n-1,r-1) + C (n-1,r) , en los
demás casos;
ii) un procedimiento por programación dinámica, en
donde directamente se construye el triángulo de
Tartaglia hasta el nivel requerido.
Por ejemplo, para el número combinatorio C (30,12)
constatamos k1=172.986.449 llamadas de recursión,
las cuales se reducen a k2=930 operaciones por
programación dinámica.
keywords: algoritmos
- trilistado.pas
-
El `tri-listado' de un arbol ordenado binario puede
pensarse como una combinacion de los listados previo,
posterior y simetrico. Asumamos que las etiquetas tienen
tres partes, una etiqueta `derecha', una `izquierda' y
otra 'centro', entonces el tri-listado de un nodo n se
define como:
TRI_LISTADO (n) = (ETIQ_IZQ (n), TRI_LISTADO (HIJO_IZQ (n)),
ETIQ_CENTRO (n), TRI_LISTADO (HIJO_DER(n)), ETIQ_DER (n)).
Por ejemplo, si A: 1 ( 8 ( 3 2 ) 4 ( 9 2 ) ), y tomamos como
etiqueta derecha a (100+etiqueta) y etiqueta izquierda como
(200+etiqueta), entonces debe listar (1 8 3 103 203 108 2
102 202 208 101 4 9 109 209 104 2 102 202 204 201). Para
simplificar, en vez de tener 3 etiquetas tenemos una sola
etiqeta entera `e'. La etiqueta del centro es (100+e) y la
derecha es (200+e). Por ejemplo si la etiqueta es 11
entonces las etiquetas izquierda, centro y derecha son
[11,111,211]. [Tomado 2do parcial de 2003, 3-Jun-2003].
Keywords: arbol binario
- verifsum.pas
-
En un programa de diseño asistido por computadora
(tipo AutoCAD) se desea mantener las piezas de un sistema
(por ejemplo un auto) clasificando sus partes en la forma
de un árbol, donde sus nodos interiores representan
sistemas del auto (planta motriz, direccion, carroceria),
sus hijos subs-sistemas y asi siguiendo hasta las hojas
que son los componentes indivisibles del automovil (por
ej. el tornillo de fijación del espejo retrovisor
izquierdo).
Se quiere mantener en cada hoja el peso (en Kilogramos)
del componente, y en los nodos interiores el peso total
de todos los componentes del subárbol que cuelga de ese
nodo. Periódicamente se quiere verificar que efectivamente
las etiquetas del árbol verifican esta propiedad, es
decir que la etiqueta de los nodos interiores es la
suma de las hojas del subárbol que cuelga de él.
Escribir una function VERIFICA_SUMA (n: nodo; A: Arbol):
boolean; que retorna true si el subarbol que cuelga del nodo
verifica la condicion dada y false en caso contrario. Usar
las primitivas del `TAD ARBOL ORDENADO ORIENTADO':
`HIJO_MAS_IZQ (n,A)', `HERMANO_DER (n,A)',`ETIQUETA (n,A)'.
[Tomado en el segundo parcial del cursado 2002, 28/5/2002.]
keywords: arbol orientado
- viajant1.pas
-
Problema del viajante mediante un algoritmo ávido
versión 1.
keywords: algoritmos
- viajant2.pas
-
Problema del viajante mediante un algoritmo ávido,
versión 2. keywords: algoritmos
- arbbtools.pas
-
Herramientas auxiliares para árboles binarios
por cursores. keywords: arbol binario, cursores
- ordnodo.pas
-
Escribir una function ORDNODO (n: nodo, A:arbol): boolean;
que verifica si cada secuencia de hermanos del subarbol
del nodo "n" (perteneciente al arbol ordenado orientado A)
estan ordenadas entre si, de izquierda a derecha. Por
ejemplo, ver figura, para el arbol de la izquierda deberia
retornar "true", mientras que para el de la derecha deberia
retornar "false", ya que las secuencias de hermanos
indicados en las rayadas NO estan ordenados. Se sugiere el
siguiente algoritmo: para un dado nodo retornar false si:
1) sus hijos no estan ordenados o 2) algunos de sus hijos
contiene en su subarbol una secuencia de hermanos no
ordenada (recursividad).
[Tomado 2do parcial de 2003, 3-Jun-2003]
keywords: arbol orientado
- u_arbbii.pas
-
Arboles binarios de enteros por cursores.
keywords: arbol binario, cursores
- u_arbbir.pas
-
Arboles binarios de reales por cursores.
keywords: arbol binario, cursores
- u_arbori.pas
-
Arbol ordenado y orientado de enteros por cursores.
keywords: arbol orientado, cursores
- u_arborip.pas
-
Arbol ordenado y orientado de enteros por punteros. Esta
implementación introduce primitivas adicionales para
crear y modificar árboles. Las rutinas CREAi son muy
``rigidas'' para crear arboles entonces se proponen las
funciones AGREGA_HIJO_MAS_IZQ, AGREGA_HERM_DER,
CORTA_PEGA_HIJO_MAS_IZQ y CORTA_PEGA_HERM_DER que
permiten crear y modificar el árbol en una forma
mucho mas ágil.
keywords: arbol orientado, punteros
- u_arborr.pas
-
Arbol ordenado y orientado de reales por cursores.
keywords: arbol orientado, cursores
- u_colaai.pas
-
Colas de enteros por arreglos.
keywords: cola, arreglos
- u_colaar.pas
-
Colas de reales por arreglos.
keywords: cola, arreglos
- u_colapc.pas
-
Colas de caracteres (simples) por punteros.
keywords: cola, punteros
- u_colapi.pas
-
Colas de enteros por punteros.
keywords: cola, punteros
- u_colapr.pas
-
Colas de reales por punteros.
keywords: cola, punteros
- u_colexp.pas
-
Cola de expresión usada en evaluación de expresiones
algebraicas. keywords: cola
- u_colpar.pas
-
Cola de pares de enteros por punteros.
keywords: cola, punteros
- u_cuchar.pas
-
Unidad auxiliar para conjuntos por arreglos de bits: con
las funciones INDICE/ELEMENTO y el procedimiento IMPRIME,
cuando el conjunto universal es el Alfabeto a-z
[Usada por u_setvbi.pas]
keywords: conjunto
- u_dcolpi.pas
-
Doble cola por punteros. keywords: cola, punteros
- u_liscif.pas
-
Listas de enteros por cursores, con celdas de
encabezamiento y cursores al final (mucho mejor
que 'u_listci'). keywords: lista, cursores
- u_liscrf.pas
-
Listas de reales por cursores, con celdas de
encabezamiento y cursores al final (mucho mejor
que 'u_listcr'). keywords: lista, cursores
- u_lispif.pas
-
Lista de enteros por punteros. Incluye un puntero a la
celda final, para reducir el orden de las operaciones en
la función FIN. También hace los dispose de las celdas
liberadas tanto en SUPRIME como en ANULA.
keywords: lista, punteros
- u_lisprf.pas
-
Lista de reales por punteros. Incluye un puntero a la
celda final, para reducir el orden de las operaciones en
la función FIN. También hace los dispose de las celdas
liberadas tanto en SUPRIME como en ANULA.
keywords: lista, punteros
- u_listai.pas
-
Listas de enteros por arreglos. keywords: lista, arreglos
- u_listar.pas
-
Listas de reales por arreglos. keywords: lista, arreglos
- u_listci.pas
-
Listas de enteros por cursores y sin celdas de
encabezamiento.
- u_listcr.pas
-
Listas de reales por cursores y sin celdas de
encabezamiento. keywords: lista, cursores
- u_listpi.pas
-
Listas de enteros por punteros. keywords: lista, punteros
- u_listpr.pas
-
Lista de reales por punteros. keywords: lista, punteros
- u_orden2.pas
-
Unidad para clasificar (u ordenar) un vector de enteros
de menor a mayor, mediante los métodos de: BURBUJA,
INSERCION, SELECCION, SHELL, MONTICULO y RAPIDO.
keywords: clasificacion
- u_pilap.pas
-
Pilas de __TIPO_EN_ESPANOL__ por punteros. keywords: pila
- u_pilapc.pas
-
Pilas de caracteres por punteros. keywords: pila
- u_pilapi.pas
-
Pilas de enteros por punteros. keywords: pila
- u_pilapr.pas
-
Pilas de reales por punteros. keywords: pila
- u_prique.pas
-
Colas de prioridad por monticulos. keywords: cola de prioridad
- u_setlis.pas
-
Conjuntos como listas. keywords: lista, conjunto
- u_setvbi.pas
-
Conjuntos como arreglos de bits. keywords: conjunto
- u_shasc2.pas
-
TAD-DICCIONARIO (Inserta, Suprime, Miembro, Anula)
para enteros, con dispersión cerrada: ya sea con
resolución lineal (redisp1) o bien con resolución
pseudo-aleatoria (redisp2) de las colisiones.
En el procedimiento CONJ.ALEINI se calculan todas las
constantes d para un dado B (potencia de 2), a partir
de los k admisibles ya tabulados, los cuales fueron
hallados previamente por el programa ``ALEANUM1''.
keywords: conjunto
- u_shasci.pas
-
TAD-DICCIONARIO (Inserta, Suprime, Miembro, Anula)
con dispersión cerrada y resolución lineal de
colisiones, para enteros.
keywords: conjunto, tabla de dispersion
- u_shashi.pas
-
TDA-Diccionario (Inserta, Suprime, Miembro, Anula)
con dispersión abierta, para enteros.
keywords: conjunto, tabla de dispersion